MECÁNICA DE SÓLIDOS
TEMAS Y SUBTEMAS
1.1. Elemento diferencial
1.2. Simetría del tenso de esfuerzos
1.3. Esfuerzos
1.3.1. En dos
dimensiones
1.3.1.1. Deformación plana
1.3.1.2. Esfuerzo plano
1.3.1.3. Principales
esfuerzos
1.3.2. En tres
dimensiones
1.3.2.1. En cilindros de
pares gruesas sujetas a presión interna y externa
1.3.2.2. Radiales
1.3.2.3. Máximos en vigas
curvas
1.4. Planos principales
1.5. Interpretación gráfica del tensor de esfuerzos, mediante el círculo de
Mohr
1.6. Tensores de esfuerzo
1.6.1. Generado por
carga axial
1.6.2. Generado por
carga cortante
1.6.3. Generado por
momento torsor
1.6.4. Generado por
momento flexor
1.6.5. Generado por
presiones internas
1.6.6. Generado por
solicitaciones combinadas
2. ESTADO GENERAL DE DEFORMACIONES
2.1. Concepto de
desplazamiento de cuerpo
2.1.1. Traslación
2.1.2. Rotación
2.1.3. Alargamiento
2.2. Características
de la deformación en un elemento diferencial
2.3. Estado general
de deformaciones
2.3.1. Distorsión
2.3.2. Deformaciones
principales
2.4. Interpretación de un estado de deformaciones del círculo de Mohr
3. LEY GENERALIZADA
DE HOOKE
3.1. Modulo de Young
3.2. Modulo de Poisson
3.3. Modulo de
Cortante
3.4. Constante
volumétrica
3.5. Isotropía en
materiales
3.6. Relaciones
esfuerzo – deformación para materiales elásticos
4. MÉTODOS
ENERGÉTICOS
4.1. Energía de
deformación en los elementos simples sujetos a carga axial
4.2. Aplicaciones del
teorema de Castigliano
5. COLUMNAS, UNIONES
Y ESFUERZOS
5.1. Columnas con
carga concéntrica
5.2. Columnas con
carga excéntrica
5.3. Resistencia de
juntas múltiples
5.4. Clasificación de
los materiales aporte y características
5.5. Resistencia de
juntas con carga excéntrica
5.6. Uniones
remachadas o atornilladas
5.7. Clasificación de
los elementos de sujeción
5.8. Resistencia de
juntas múltiples
5.9. Resistencia de
juntas con carga excéntrica
|
1. ESTADO GENERAL DE
ESFUERZOS
Los Esfuerzos Combinados
son aquellos que actúan en una sección de un elemento cuando
existe una combinación de dos o más de las acciones internas actuando en dicho
elemento. Los esfuerzos combinados representan la suma o combinación de
esfuerzos de carga axial, esfuerzos por carga de deflexión y esfuerzo por carga
de torsión. En la representación de los esfuerzos combinados, por lo general
los elementos analizados no están sometidos a un solo tipo de esfuerzo, si no,
más bien a la interacción de varios esfuerzos de manera simultánea, es por ello
que con la finalidad de localizar el punto donde la estructura llegaría a
fallar (punto critica de la estructura), se analiza la interacción de todos los
esfuerzos a los que está sometido el elemento. También es método para
dimensionar y seleccionar el material adecuado por el elemento.
En general, no es posible encontrar directamente los valores
de los esfuerzos en un plano que tenga una dirección cualquiera. En vigas, por
ejemplo, la flexión da los valores del esfuerzo normal que aparecen en un plano
perpendicular al eje de la viga. En torsión, se puede calcular el esfuerzo
cortante en planos perpendiculares al eje de la barra.
Existen dos +pos principales de fuerzas en un conjunto:
1. Fuerzas de cuerpo. Actúan en cualquier parte del cuerpo y son
proporcionales al volúmen o a la masa.
2. Fuerzas de superficie. Si imaginamos que quitamos el material que está
afuera del volúmen V, encontramos que hay otras fuerzas que son
proporcionales a cada elemento de superficie.
1.1 ELEMENTO DIFERENCIAL
Tanto el elemento diferencial de área como el
elemento diferencial de línea, pueden ser considerados casos particulares del
elemento diferencial de volumen. Partiendo de las ecuaciones paramétricas del
volumen, la obtención de su elemento diferencial es inmediata, en consecuencia
también es inmediata la obtención de los elementos diferenciales de área y
línea. A partir de los elementos diferenciales generales se puede determinar
cualquier caso particular, por ejemplo, cuando las ecuaciones vienen dadas en
su forma cartesiana. En los cambios de variable en integrales triples, dobles,
o simples, siempre hay que multiplicar el producto de los diferenciales por el
jacobiano de la transformación. El método de enseñanza es más sencillo, ya que
desde lo general, cuya obtención no es complicada, se llega a lo particular.
1.2 SIMETRÍA DEL TENSO DE ESFUERZOS
La simetría es un rasgo característico de formas geométricas, sistemas, ecuaciones y otros objetos materiales, o entidades abstractas, relacionada con su invariancia bajo ciertas transformaciones, movimientos o intercambios. e por tal motivo que la simetría en tensor de esfuerzo es crucial para la aplicación de esfuerzos
1.3
EL ESFUERZO
Es la fuerza que actualmente sobre el área unitaria
de un cuerpo existen diversos tipos de esfuerzo:
Tension
El esfuerzo se suele representar en Pascales
(pa) o en psi (libras por pulgadas cuadradas).
1.3.1. EN DOS DIMENSIONES
Un sistema de
esfuerzos el cual consiste solamente de esfuerzos normales y de esfuerzos
cortantes los cuales son funcionarios de X y Y se considera un sistema de dos
dimensiones o sistema de esfuerzo plano.
Teoria del circulo de mohor para dos dimensiones
se considera un cuerpo sobre el cual actualmente un estado plano de cargas.
considerando este como plano xy, de modo que existan esfuerzos en el sentido
perpendicular a este (esfuerzos nulos en z) supongamos que existe un elemento
triangular donde se supone que los ejes x e y, son los principales, esto quiere
decir que las tensiones de corte en ese plano son nulas.
1.3.1.1 DEFORMACIÓN PLANA
Ley de Hooke para deformación plana
1.3.1.3 ESFUERZOS PRINCIPALES
Para cualquier punto sometido a esfuerzos existen tres
planos ortogonales en los cuales los esfuerzos tangenciales son nulos,
estos planos se denominan Planos Principales. El mayor de estos tres esfuerzos se denomina esfuerzo principal mayor
el menor es el es fuerzo principal menor y el tercero es el esfuerzo principal
intermedio
1.3.2 ESFUERZO
EN TRES DIMENSIONES
Los esfuerzos se pueden representar en 3-D, podemos imaginarnos un cubo
y sobre el describir los esfuerzos en el sistema coordenado.
Los esfuerzos normales y esfuerzos
cortantes o de cizalle en las tres
direcciones (x,y,z) y en las tres caras del cubo que estamos imaginando
1.3.2.1. EN
CILINDROS DE PARES GRUESAS SUJETAS A PRESIÓN INTERNA Y EXTERNA
Un cilindro se considera de paredes
gruesas si el espesor de su pared es mayor que una décima parte de su radio
medio. En estos casos, las variaciones de tensión entre la superficie interior
y exterior se hacen apreciables, y las fórmulas ordinarias de tensión media no
son aceptables.
1.3.2.1. EN
CILINDROS DE PARES GRUESAS SUJETAS A PRESIÓN INTERNA Y EXTERNA
Un cilindro se considera de paredes
gruesas si el espesor de su pared es mayor que una décima parte de su radio
medio. En estos casos, las variaciones de tensión entre la superficie interior
y exterior se hacen apreciables, y las fórmulas ordinarias de tensión media no
son aceptables.
1.3.2.2 ESFUERZOS RADIALES
Son esfuerzos de dirección normal a la
dirección que pasa por el centro de su eje, como por ejemplo una rueda, es
axial si soporta esfuerzos en la dirección de su eje, ejemplo en quicio, y
axial-radial si los puede soportar en los dos, de forma alternativa o
combinada.

1.3.2.3
MÁXIMOS EN VIGAS Y CURVAS
La teoría de vigas a flexión,
presentada en el tema de flexión pura, está limitada a vigas rectas o vigas
levemente curvas con respecto a su altura. Sin embargo, si la relación del
radio de curvatura a la profundidad de (altura) es menor a 5, la fórmula de
flexión (Flexión pura) es generalmente inadecuada para describir los esfuerzos
de flexión en la viga. Para vigas curvas, la teoría de flexión también debe
tomar en consideración la curvatura. En este capítulo es desarrollada una
teoría basada en métodos de mecánica de los materiales. Resultan dos
diferencias importantes con respecto a las vigas rectas a flexión. Primero, la
distribución de esfuerzo flector en una viga curva no es lineal, basado en este
resultado, el eje neutro no coincidirá con el eje centroidal de la sección
transversal, cuando la viga esté sometida a flexión pura. Segundo, una viga
curva conlleva esfuerzos radiales como una consecuencia del momento flector
interno. Estos esfuerzos radiales tienen importantes implicaciones de diseño
para secciones transversales de pared delgada y para materiales (tales como
madera y compuestos unidireccionales) con esfuerzo de tensión relativamente
bajos en la dirección radial.
1.4 PLANOS PRINCIPALES
Los esfuerzos normales y cortantes en
el punto variarán con la dirección en cualquier sistema de coordenadas que se
escoja. Siempre habrá planos sobre los cuales las componentes de esfuerzo
cortante sean igual a cero. Los esfuerzos normales que actúan sobre esos planos
se conocen como esfuerzos
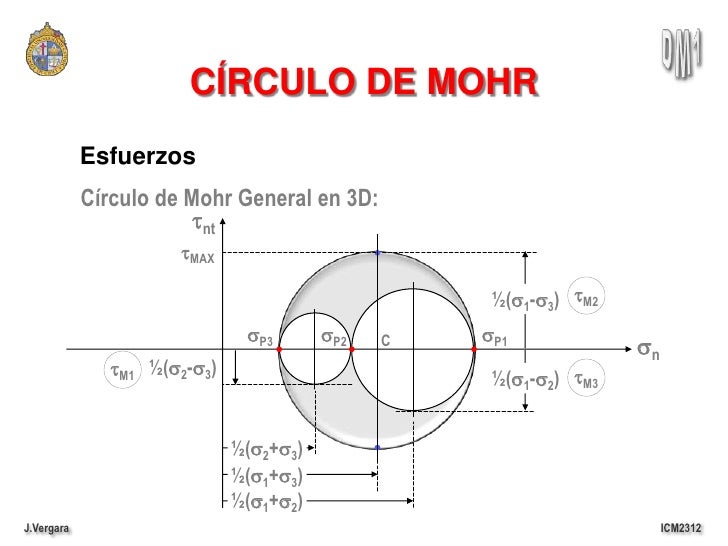
1.5. INTERPRETACIÓN
GRÁFICA DEL TENSOR DE ESFUERZOS, MEDIANTE EL CÍRCULO DE MOHR
Los círculos de Mohr son un método para representar gráficamente el
estado tensional que padece un punto de un sólido en un instante determinado.
Aunque actualmente, gracias a los ordenadores, es posible calcular las
tensiones con gran precisión sin recurrir a estos métodos, siguen siendo de
gran validez puesto que de un solo golpe de vista hacen comprensible la
situación tensional del sólido.
figura..

2.1 CONCEPTO
DE DESPLAZAMIENTO DE UN CUERPO

Crédito de la imagen: Openstax College Physics
2.1.1
TRASLACION
El término que nos ocupa está compuesto por dos vocablos
cuyos orígenes etimológicos coinciden pues ambos provienen del latín. Así,
movimiento procede de movere y traslación emana de translatio que puede definirse
como la acción de llevar algo de un lado a otro.
El estado de aquel objeto que está cambiando de sitio se
conoce como movimiento. El término está vinculado al verbo mover, que refiere a
conseguir que algo salga de la posición que ocupa y se traslade a una distinta.
Sacudir algo también se conoce como mover.
Traslación, por su parte, es un concepto con varios usos.
Puede tratarse del proceso y de las consecuencias de trasladar una cosa o una
persona de un espacio a otro; de una clase de figura retórica; de la traducción
a un idioma diferente; o del movimiento desarrollado por un cuerpo que traza
una curva de amplio radio respecto a sus dimensiones propias.

2.1.2 ROTACION
Rotación alrededor de un eje fijo es un caso especial del movimiento rotacional. La
hipótesis del eje fijo excluye la posibilidad de un eje en movimiento, y no puede
describir fenómenos como el “bamboleo”.

s=θR
v=ωR
a=αR
Para la cinemática del movimiento rotacional utilizaremos las
siguientes:
2.3.1 DISTORSIÓN
1. Alteración de un hecho falseando la realidad calificó de distorsión de la historia a lascrónicas medievales.
Torcedura o distensión violenta de una articulación sin dislocación del hueso,con posible rotura de algún ligamento o de fibras musculares. Torcedura, esguince
Deformación de una onda óptica o acústica durante su propagación.

2.3.2 DEFORMACIONES PRINCIPALES
Al ser el tensor de pequeñas
deformaciones simétrico, se puede afirmar que existirán en cada punto del
sólido elástico tres direcciones perpendiculares entre sí, correspondientes a
sendos planos, en los que no hay distorsión o deformación angular.
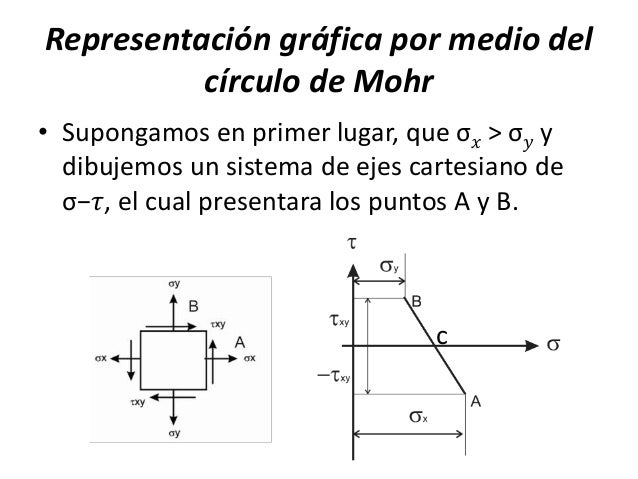
2.4 INTERPRETACION
DE UN ESTADO DE DEFORMACIONES DEL CIRCULO DE MOHR
El concepto de círculo de Mohr puede
extenderse al análisis de deformaciones planas ya que las ecuaciones de
transformación tienen la misma forma que las asociadas a la transformación de
tensiones. Por lo tanto, se tiene la relación:
°c Gelacio Juárez, UAM
3. LEY GENERALIZADA DE HOOKE
INTRODUCCION
La Estática es la parte de la mecánica que estudia las condiciones que deben cumplirse para que un cuerpo, sobre el que actúan fuerzas, permanezca en equilibrio.
Bajo la acción de una fuerza externa, un cuerpo puede sufrir una deformación que origina que cambie de forma o tamaño. Un cuerpo es elástico si este recupera su forma o tamaño original cuando desaparecen las fuerzas aplicadas. Si por el contrario, la fuerza aplicada causa que el cuerpo sobrepase su límite elástico, la deformación que ocurre es irreversible y el cuerpo no retoma su forma y tamaño original. El máximo esfuerzo que un material puede soportar antes de quedar permanentemente deformado se denomina límite de elasticidad.
Un caso particular de elasticidad es cuando se aplica una fuerza variable a un objeto. El caso más conocido, y cuyo comportamiento refleja muchos fenómenos naturales, es el de un resorte.
LEY DE HOOKE
Esta ley describe fenómenos de tipo elástico, como el que se origina cuando una fuerza externa se aplica a un resorte. La ley establece que “La fuerza que devuelve un resorte a su posición de equilibrio es proporcional al valor de la distancia que se desplaza de esa posición”. La figura siguiente muestra un resorte en su estado de reposo (a), esto es, sin compresión o extensión. Uno de los extremos está fijo, y tiene un cuerpo unido en el extremo libre.
En buena aproximación en la mayoría de los resortes, la fuerza 𝐹! desde el resorte es proporcional al desplazamiento 𝑑 del extremo del resorte relativo al estado de reposo. La fuerza del resorte está dada por:
3.1 MODULO DE YOUNG
El módulo de elasticidad o módulo de Young es un parámetro que caracteriza el comportamiento de un material elástico, según la dirección en la que se aplica una fuerza. Para un material elástico lineal e isótropo, el módulo de Young tiene el mismo valor para una tracción que para una compresión, siendo una constante independiente del esfuerzo siempre que no exceda de un valor máximo denominado límite elástico, y es siempre mayor que cero: si se tracciona una barra, aumenta de longitud, no disminuye. Este comportamiento fue observado y estudiado por el científico inglés Thomas Young.
Tanto el módulo de Young como el límite elástico son distintos para los diversos materiales. El módulo de elasticidad es una constante elástica que, al igual que el límite elástico, puede encontrarse empíricamente con base al ensayo de tracción del material.
3.2 MODULO DE POISSON
El coeficiente de Poisson es una constante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento.
Se conoce a la relación de Poisson, cuando un cuerpo se somete a una fuerza, este siempre se deformara en dirección a esta fuerza. Sin embargo, siempre que se producen deformaciones en dirección de la fuerza aplicada, también se producen deformaciones laterales. Las deformaciones laterales tienen una relación constante con las deformaciones axiales, por lo que esta relación es constante, siempre que se el material se encuentre en el rango elástico de esfuerzos, o sea que no exceda el esfuerzo del límite proporcionalidad.
Esfuerzo Cortante:
Factor de elasticidad de un material
que representa la relación entre el esfuerzo cortante y la correspondiente
deformación producida por éste. También llamado módulo de elasticidad
transversal.
Constante Volumétrica
Es aquella en que predomina la
variación en tres dimensiones, o sea, la variación del volumen del cuerpo, este
fenómeno se ve dado por la siguiente formula;
Isotropía en materiales
Un material es isótropo cuando sus propiedades no dependen de la dirección
según la cual ellas son medidas. Una propiedad tiene el mismo valor
independiente de la dirección según la cual se hace la medida. Los materiales
amorfos (o no cristalinos) son estrictamente isótropos. Ello se debe a que no
presentan direcciones que difieran entre sí en su tipo de orden atómico lineal,
por no haber orden cristalino. Isotropía por compensación en policristales
Frecuentemente en ingeniería, particularmente para aplicaciones estructurales,
se emplean policristales. En ocasiones, los policristales formados por muchos
granos (granos que son monocristales anisótropos), pueden ser considerados, en
promedio, como isótropos, según se verá. Particularmente cuando la estructura
de un policristal está recocida, se pueden tener granos con las siguientes tres
características de estos: Finos: el tamaño de grano es suficientemente pequeño
como para que, en la sección consi-derada haya muchos granos. De forma
equiaxial: en el material no hay direcciones preferenciales al mirar los
granos, por ejemplo, en un microscopio óptico. Con orientaciones cristalinas al
azar: por ejemplo, en un policristal de cobre, de estructura CCC, los ejes
OX-OY-OZ de distintos granos, ejes correspondientes a las aristas de las celdas
cristalinas respectivas, están orientados al azar.
UNIONES REMACHADAS O
ATORNILLADAS
Uniones por remaches.
El remache, como elemento
de fijación, consiste en un tubo cilíndrico (el vástago) con una cabeza en
un extremo y que al deformar el extremo opuesto, mediante presión o un
golpe, se obtiene otra cabeza que ejerce presión sobre la cara opuesta de
la fijación, en consecuencia los elementos implicados en esta unión quedan
unidos con una presión que dependerá de la presión aplicada por el
propio remache y las propiedades del material. Un tipo específico de
remaches son los roblones, remaches con diámetro superior a 10mm y que a
la hora de efectuar el remachado se calientan para facilitar
su deformación
Montaje de las uniones remachadas.
Para realizar el r emachado primero se
perfora la chapa a unir, se coloca el remache (frio o caliente) en la
perforación y se conforma la otra cabeza. El proceso de remachado pude ser
realizado en caliente, normalmente para obras pequeñas realizadas en
taller, o para remaches grande, o puede realizarse en frio, para
remachados en campo. Inicialmente la cabeza de los remaches se conseguía a
golpe de martillo, actualmente todo está simplificado por el uso de
maquinaria especial. Los remaches acostumbran a ser de metal, acero
de bajo contenido en carbono, o de aluminio por ser más dúctiles.
Uniones atornilladas
Funcionan en las construcciones
desmontables y en la unión de elementos construidos en taller al llegar a
la obra para facilitar su transporte y montaje.
5.7 Clasificasion De Los
Elementos De Sujecion
Como elementos de sujeción se
entienden, en primer lugar, tornillos y tuercas de todas formas y variaciones.
Sin embargo, también se incluyen ganchos, cáncamos, bulones y remaches como
elementos que deben mantenerse unidos bajo cargas determinadas. La técnica de
uniones en general y la técnica de soldadura en especial se incluyen en este
grupo.
Ensayo de
tracción de uniones atornilladas
Los tornillos son productos que se
eligen con mucha precisión para la aplicación industrial, con el fin de
adaptarlas a la construcción correspondiente. Para la seguridad de la unión
atornillada es imprescindible la determinación exacta del módulo elástico y de
los límites de la carga elástica durante ensayos de tracción, ya que de ellos
se deducen las fuerzas límite para una unión atornillada segura. Debido al
sinfín de aplicaciones existe un sinfín de tornillos y tipos de tornillos de lo
más diverso. Zwick ofrece soluciones mediante muchas sujeciones diferentes y
también con soluciones individuales.
Ensayo de cizallamiento
Aparte de cargas uniaxiales de
tracción, los elementos de sujeción se encuentran sometidos en la práctica a
cargas de cizallamiento que pueden causar una rápida rotura de la unión.
Ensayo de fatiga en tornillos
COLUMNAS,
UNIONES Y ESFUERZOS
5.1 Columnas con cargas concéntricas
COLUMNAS
5.2 Columnas con cargas excéntricas
Cargas excéntricas Las cargas
excéntricas pueden resultar por una carga aplicada fuera del centro de la
zapata o de una carga concéntrica más un momento flexor. Para determinar la
presión debajo de una zapata el momento puede ser removido desplazando la carga
vertical a una locación ficticia con una excentricidad e=m\carga vertical. En
el análisis de cargas excéntricas de zapatas dos diferentes problemas son
confrontados uno.
5.3 RESISTENCIA DE JUNTAS MULTIPLES
La resistencia a cortante en las
juntas secas es una parte importante del diseño de estructuras de dovelas
postensadas. Sin embargo, la formulación de las distintas normativas no se
ajusta al comportamiento de las juntas con llaves múltiples. En este trabajo se
analiza el comportamiento en fractura de las juntas secas con llaves bajo
solicitaciones de cortante, centrándose en la influencia del número de llaves
en la resistencia de la junta y la tensión tangencial media. Para ello, se
modeliza en elementos finitos cuatro tipos de junta, de una a siete llaves. Los
resultados muestran que la tensión tangencial media transferida por la junta
disminuye al aumentar el número de llaves, siendo este efecto menor conforme
aumenta la tensión de compresión actuante en la junta. En este trabajo se
presenta una fórmula de ajuste de los resultados numéricos obtenidos incluyendo
un factor que considera la dependencia del número de llaves.
5.4 Clasificación de los materiales
aporte y características
Se entiende como material de
aportación, todo aquel material que se utiliza para la realización de un cordón
de soldadura de buena calidad y donde distinguimos, por un lado, el núcleo del
electrodo y el revestimiento, y, por otro lado, la varilla de aporte y los
fundentes, estos los usaremos en función del tipo de soldadura que vayamos a
realizar.
5.5 Resistencia de juntas con carga
excéntrica
Cuando la carga sobre una junta
soldada se aplica excéntricamente, el efecto del par o momento debe tomarse en
cuenta, así como la carga directa. El estado de esfuerzo en tal junta es
complicado y es necesario hacer hipótesis simplificadoras.
BIBLIOHGRAFIAS
1.3
EL ESFUERZO
1.3.1. EN DOS DIMENSIONES
Un sistema de
esfuerzos el cual consiste solamente de esfuerzos normales y de esfuerzos
cortantes los cuales son funcionarios de X y Y se considera un sistema de dos
dimensiones o sistema de esfuerzo plano.
Teoria del circulo de mohor para dos dimensiones
se considera un cuerpo sobre el cual actualmente un estado plano de cargas. considerando este como plano xy, de modo que existan esfuerzos en el sentido perpendicular a este (esfuerzos nulos en z) supongamos que existe un elemento triangular donde se supone que los ejes x e y, son los principales, esto quiere decir que las tensiones de corte en ese plano son nulas.
1.3.1.1 DEFORMACIÓN PLANA
Ley de Hooke para deformación plana
Para esos casos en que los componentes de deformación se encuentran contenidas en uno
de los planos de la fibra (por ejemplo en el plano XY), la ley de Hooke
generalizada también puede ser expresada de forma más simple
Si bien la deformación plana y el esfuerzo plano tienen cada
uno tres componentes en el mismo plan
o, téngase en cuenta que es el esfuerzo
plano no necesariamente fuera deformación plano o viceversas. Esto se debe al
efecto de la razón de poisson.
1.3.1.3 ESFUERZOS PRINCIPALES
Para cualquier punto sometido a esfuerzos existen tres
planos ortogonales en los cuales los esfuerzos tangenciales son nulos,
estos planos se denominan Planos Principales. El mayor de estos tres esfuerzos se denomina esfuerzo principal mayor
el menor es el es fuerzo principal menor y el tercero es el esfuerzo principal
intermedio
1.3.2 ESFUERZO
EN TRES DIMENSIONES
Los esfuerzos se pueden representar en 3-D, podemos imaginarnos un cubo
y sobre el describir los esfuerzos en el sistema coordenado.
Para determinar el estado de esfuerzos en un punto se deben definir los
esfuerzos orientados en 3 dimensiones ortogonales entre sí. Esta descripción se
hace mediante el tensor de esfuerzos, que relaciona el vector F (3 componentes)
con el área unitaria A (3 componentes). De los 9 componentes resultantes, 3
actúan perpendicularmente a la superficie (esfuerzos normales, σn) (σii), i= x,
y, z), y 6 actúan en la dirección paralela a dicha superficie (esfuerzos de
cizalla, τ)
Los esfuerzos normales y esfuerzos
cortantes o de cizalle en las tres
direcciones (x,y,z) y en las tres caras del cubo que estamos imaginando
1.3.2.1. EN
CILINDROS DE PARES GRUESAS SUJETAS A PRESIÓN INTERNA Y EXTERNA
Un cilindro se considera de paredes gruesas si el espesor de su pared es mayor que una décima parte de su radio medio. En estos casos, las variaciones de tensión entre la superficie interior y exterior se hacen apreciables, y las fórmulas ordinarias de tensión media no son aceptables.

1.3.2.1. EN
CILINDROS DE PARES GRUESAS SUJETAS A PRESIÓN INTERNA Y EXTERNA
Un cilindro se considera de paredes
gruesas si el espesor de su pared es mayor que una décima parte de su radio
medio. En estos casos, las variaciones de tensión entre la superficie interior
y exterior se hacen apreciables, y las fórmulas ordinarias de tensión media no
son aceptables.
1.3.2.2 ESFUERZOS RADIALES
Son esfuerzos de dirección normal a la
dirección que pasa por el centro de su eje, como por ejemplo una rueda, es
axial si soporta esfuerzos en la dirección de su eje, ejemplo en quicio, y
axial-radial si los puede soportar en los dos, de forma alternativa o
combinada.
1.3.2.3
MÁXIMOS EN VIGAS Y CURVAS
La teoría de vigas a flexión,
presentada en el tema de flexión pura, está limitada a vigas rectas o vigas
levemente curvas con respecto a su altura. Sin embargo, si la relación del
radio de curvatura a la profundidad de (altura) es menor a 5, la fórmula de
flexión (Flexión pura) es generalmente inadecuada para describir los esfuerzos
de flexión en la viga. Para vigas curvas, la teoría de flexión también debe
tomar en consideración la curvatura. En este capítulo es desarrollada una
teoría basada en métodos de mecánica de los materiales. Resultan dos
diferencias importantes con respecto a las vigas rectas a flexión. Primero, la
distribución de esfuerzo flector en una viga curva no es lineal, basado en este
resultado, el eje neutro no coincidirá con el eje centroidal de la sección
transversal, cuando la viga esté sometida a flexión pura. Segundo, una viga
curva conlleva esfuerzos radiales como una consecuencia del momento flector
interno. Estos esfuerzos radiales tienen importantes implicaciones de diseño
para secciones transversales de pared delgada y para materiales (tales como
madera y compuestos unidireccionales) con esfuerzo de tensión relativamente
bajos en la dirección radial.
1.4 PLANOS PRINCIPALES
Los esfuerzos normales y cortantes en
el punto variarán con la dirección en cualquier sistema de coordenadas que se
escoja. Siempre habrá planos sobre los cuales las componentes de esfuerzo
cortante sean igual a cero. Los esfuerzos normales que actúan sobre esos planos
se conocen como esfuerzos
1.5. INTERPRETACIÓN
GRÁFICA DEL TENSOR DE ESFUERZOS, MEDIANTE EL CÍRCULO DE MOHR
Los círculos de Mohr son un método para representar gráficamente el
estado tensional que padece un punto de un sólido en un instante determinado.
Aunque actualmente, gracias a los ordenadores, es posible calcular las
tensiones con gran precisión sin recurrir a estos métodos, siguen siendo de
gran validez puesto que de un solo golpe de vista hacen comprensible la
situación tensional del sólido.
Se organiza con sus ejes mutuamente perpendiculares, aunque en el
espacio real el ángulo entre ellos representa 180º. Todos los ángulos dibujados
en el plano de Mohr tienen el doble de su valor en el espacio real. La abscisa
es el eje para todos los esfuerzos normales. Los esfuerzos normales aplicados
σx, σy y σz, se trazan a lo largo de este eje y los esfuerzos principales σ1,
σ2 y σ3 también se determinan sobre este eje.
figura..
2.1 CONCEPTO
DE DESPLAZAMIENTO DE UN CUERPO
El desplazamiento es el movimiento para trasladarse de un lugar a
otro, o sustitución de una persona en el cargo, puesto o lugar que
ocupa. El desplazamiento también es considerado como la variación de la
posición de un cuerpo. En el ámbito de la física, el desplazamiento
es un vector cuyo origen es la posición del cuerpo en un instante
de tiempo que
se considera inicial, y cuyo extremo es la posición del cuerpo en un instante
considerado final. Cabe señalar, que el desplazamiento no depende de la
trayectoria seguida por el cuerpo sino sólo de los puntos donde se
encuentre en los instantes inicial y final; es decir, la distancia entre ellos,
la cual es expresada en metros.

Crédito de la imagen: Openstax College Physics
2.1.1
TRASLACION
El término que nos ocupa está compuesto por dos vocablos cuyos orígenes etimológicos coinciden pues ambos provienen del latín. Así, movimiento procede de movere y traslación emana de translatio que puede definirse como la acción de llevar algo de un lado a otro.
El estado de aquel objeto que está cambiando de sitio se conoce como movimiento. El término está vinculado al verbo mover, que refiere a conseguir que algo salga de la posición que ocupa y se traslade a una distinta. Sacudir algo también se conoce como mover.
Traslación, por su parte, es un concepto con varios usos. Puede tratarse del proceso y de las consecuencias de trasladar una cosa o una persona de un espacio a otro; de una clase de figura retórica; de la traducción a un idioma diferente; o del movimiento desarrollado por un cuerpo que traza una curva de amplio radio respecto a sus dimensiones propias.
2.1.2 ROTACION
Rotación alrededor de un eje fijo es un caso especial del movimiento rotacional. La
hipótesis del eje fijo excluye la posibilidad de un eje en movimiento, y no puede
describir fenómenos como el “bamboleo”.
De acuerdo al teorema de la
rotación de Euler, la rotación alrededor de más de un eje al mismo
tiempo es imposible, así pues, si dos rotaciones son forzadas al mismo tiempo
en diferente eje, aparecerá un nuevo eje de rotación.Las siguientes fórmulas y
conceptos son útiles para comprender más a fondo la rotación sobre un eje fijo.
El movimiento de rotación tiene una estrecha relación con el movimiento
lineal.
s=θR
La velocidad lineal es el producto de la velocidad angular por el radio
del círculo descrito por el movimiento.
v=ωR
La aceleración tangencial es el producto de la aceleración angular por
el radio del círculo descrito por el movimiento.
a=αR
Así mismo, tomando en cuenta lo anterior, las fórmulas de la cinemática
mantienen esta misma relación.
Para la cinemática del movimiento rotacional utilizaremos las
siguientes:
2.3.1 DISTORSIÓN
1. Alteración de un hecho falseando la realidad calificó de distorsión de la historia a lascrónicas medievales.
2. MEDICINA
Torcedura o distensión violenta de una articulación sin dislocación del hueso,con posible rotura de algún ligamento o de fibras musculares. Torcedura, esguince
Torcedura o distensión violenta de una articulación sin dislocación del hueso,con posible rotura de algún ligamento o de fibras musculares. Torcedura, esguince
3. FÍSICA
Deformación de una onda óptica o acústica durante su propagación.
Deformación de una onda óptica o acústica durante su propagación.
2.3.2 DEFORMACIONES PRINCIPALES
Al ser el tensor de pequeñas
deformaciones simétrico, se puede afirmar que existirán en cada punto del
sólido elástico tres direcciones perpendiculares entre sí, correspondientes a
sendos planos, en los que no hay distorsión o deformación angular.
2.4 INTERPRETACION DE UN ESTADO DE DEFORMACIONES DEL CIRCULO DE MOHR
El concepto de círculo de Mohr puede
extenderse al análisis de deformaciones planas ya que las ecuaciones de
transformación tienen la misma forma que las asociadas a la transformación de
tensiones. Por lo tanto, se tiene la relación:

°c Gelacio Juárez, UAM
3. LEY GENERALIZADA DE HOOKE
INTRODUCCION
La Estática es la parte de la mecánica que estudia las condiciones que deben cumplirse para que un cuerpo, sobre el que actúan fuerzas, permanezca en equilibrio.
Bajo la acción de una fuerza externa, un cuerpo puede sufrir una deformación que origina que cambie de forma o tamaño. Un cuerpo es elástico si este recupera su forma o tamaño original cuando desaparecen las fuerzas aplicadas. Si por el contrario, la fuerza aplicada causa que el cuerpo sobrepase su límite elástico, la deformación que ocurre es irreversible y el cuerpo no retoma su forma y tamaño original. El máximo esfuerzo que un material puede soportar antes de quedar permanentemente deformado se denomina límite de elasticidad.
Un caso particular de elasticidad es cuando se aplica una fuerza variable a un objeto. El caso más conocido, y cuyo comportamiento refleja muchos fenómenos naturales, es el de un resorte.
LEY DE HOOKE
Esta ley describe fenómenos de tipo elástico, como el que se origina cuando una fuerza externa se aplica a un resorte. La ley establece que “La fuerza que devuelve un resorte a su posición de equilibrio es proporcional al valor de la distancia que se desplaza de esa posición”. La figura siguiente muestra un resorte en su estado de reposo (a), esto es, sin compresión o extensión. Uno de los extremos está fijo, y tiene un cuerpo unido en el extremo libre.
En buena aproximación en la mayoría de los resortes, la fuerza 𝐹! desde el resorte es proporcional al desplazamiento 𝑑 del extremo del resorte relativo al estado de reposo. La fuerza del resorte está dada por:
3.1 MODULO DE YOUNG
El módulo de elasticidad o módulo de Young es un parámetro que caracteriza el comportamiento de un material elástico, según la dirección en la que se aplica una fuerza. Para un material elástico lineal e isótropo, el módulo de Young tiene el mismo valor para una tracción que para una compresión, siendo una constante independiente del esfuerzo siempre que no exceda de un valor máximo denominado límite elástico, y es siempre mayor que cero: si se tracciona una barra, aumenta de longitud, no disminuye. Este comportamiento fue observado y estudiado por el científico inglés Thomas Young.
Tanto el módulo de Young como el límite elástico son distintos para los diversos materiales. El módulo de elasticidad es una constante elástica que, al igual que el límite elástico, puede encontrarse empíricamente con base al ensayo de tracción del material.
Tanto el módulo de Young como el límite elástico son distintos para los diversos materiales. El módulo de elasticidad es una constante elástica que, al igual que el límite elástico, puede encontrarse empíricamente con base al ensayo de tracción del material.
3.2 MODULO DE POISSON
El coeficiente de Poisson es una constante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento.
Se conoce a la relación de Poisson, cuando un cuerpo se somete a una fuerza, este siempre se deformara en dirección a esta fuerza. Sin embargo, siempre que se producen deformaciones en dirección de la fuerza aplicada, también se producen deformaciones laterales. Las deformaciones laterales tienen una relación constante con las deformaciones axiales, por lo que esta relación es constante, siempre que se el material se encuentre en el rango elástico de esfuerzos, o sea que no exceda el esfuerzo del límite proporcionalidad.
Esfuerzo Cortante:
Factor de elasticidad de un material
que representa la relación entre el esfuerzo cortante y la correspondiente
deformación producida por éste. También llamado módulo de elasticidad
transversal.
Constante Volumétrica
Es aquella en que predomina la
variación en tres dimensiones, o sea, la variación del volumen del cuerpo, este
fenómeno se ve dado por la siguiente formula;
ΔV=ᵧVoΔT
Donde;
ΔV representa el aumento
de volumen del cuerpo.
Vo representa el volumen
inicial.
ΔT es el cambio de
temperatura.
Ahora ejemplifiquemos esto para
lograr tener un mejor entendimiento.
El volumen inicial del mercurio es de
30 cm3, pero este sufre un cambio de temperatura de 10° a los 60°.
¿Cuál será su volumen final?
ΔV=ᵧVoΔT
ΔV=0.18*10-3(30 cm3) (60°-10°)
ΔV=0.27cm3
Isotropía en materiales
Un material es isótropo cuando sus propiedades no dependen de la dirección según la cual ellas son medidas. Una propiedad tiene el mismo valor independiente de la dirección según la cual se hace la medida. Los materiales amorfos (o no cristalinos) son estrictamente isótropos. Ello se debe a que no presentan direcciones que difieran entre sí en su tipo de orden atómico lineal, por no haber orden cristalino. Isotropía por compensación en policristales Frecuentemente en ingeniería, particularmente para aplicaciones estructurales, se emplean policristales. En ocasiones, los policristales formados por muchos granos (granos que son monocristales anisótropos), pueden ser considerados, en promedio, como isótropos, según se verá. Particularmente cuando la estructura de un policristal está recocida, se pueden tener granos con las siguientes tres características de estos: Finos: el tamaño de grano es suficientemente pequeño como para que, en la sección consi-derada haya muchos granos. De forma equiaxial: en el material no hay direcciones preferenciales al mirar los granos, por ejemplo, en un microscopio óptico. Con orientaciones cristalinas al azar: por ejemplo, en un policristal de cobre, de estructura CCC, los ejes OX-OY-OZ de distintos granos, ejes correspondientes a las aristas de las celdas cristalinas respectivas, están orientados al azar.
UNIONES REMACHADAS O
ATORNILLADAS
Uniones por remaches.
El remache, como elemento
de fijación, consiste en un tubo cilíndrico (el vástago) con una cabeza en
un extremo y que al deformar el extremo opuesto, mediante presión o un
golpe, se obtiene otra cabeza que ejerce presión sobre la cara opuesta de
la fijación, en consecuencia los elementos implicados en esta unión quedan
unidos con una presión que dependerá de la presión aplicada por el
propio remache y las propiedades del material. Un tipo específico de
remaches son los roblones, remaches con diámetro superior a 10mm y que a
la hora de efectuar el remachado se calientan para facilitar
su deformación
Montaje de las uniones remachadas.
Para realizar el r emachado primero se
perfora la chapa a unir, se coloca el remache (frio o caliente) en la
perforación y se conforma la otra cabeza. El proceso de remachado pude ser
realizado en caliente, normalmente para obras pequeñas realizadas en
taller, o para remaches grande, o puede realizarse en frio, para
remachados en campo. Inicialmente la cabeza de los remaches se conseguía a
golpe de martillo, actualmente todo está simplificado por el uso de
maquinaria especial. Los remaches acostumbran a ser de metal, acero
de bajo contenido en carbono, o de aluminio por ser más dúctiles.
Uniones atornilladas
Los elementos básicos de una rosca o
hilo son el diámetro exterior, el diámetro interior, el paso, el tipo de
hilo, el sentido de avance, la cantidad de entradas y el ajuste.
Funcionan en las construcciones
desmontables y en la unión de elementos construidos en taller al llegar a
la obra para facilitar su transporte y montaje.
Se llama unión atornillada al
conjunto formado por una varilla roscada y una tuerca, la varilla roscada
atraviesa libremente las piezas que se desean unir, debiendo ser fijada en
rotación y en la que únicamente gira la tuerca.
Otras veces la segunda pieza a unir
ejerce la misión de tuerca, presentando un agujero roscado, siendo, normalmente
el tornillo el que gira y se desplaza uniendo ambas piezas.
5.7 Clasificasion De Los
Elementos De Sujecion
Como elementos de sujeción se
entienden, en primer lugar, tornillos y tuercas de todas formas y variaciones.
Sin embargo, también se incluyen ganchos, cáncamos, bulones y remaches como
elementos que deben mantenerse unidos bajo cargas determinadas. La técnica de
uniones en general y la técnica de soldadura en especial se incluyen en este
grupo.
Ensayo de
tracción de uniones atornilladas
Los tornillos son productos que se
eligen con mucha precisión para la aplicación industrial, con el fin de
adaptarlas a la construcción correspondiente. Para la seguridad de la unión
atornillada es imprescindible la determinación exacta del módulo elástico y de
los límites de la carga elástica durante ensayos de tracción, ya que de ellos
se deducen las fuerzas límite para una unión atornillada segura. Debido al
sinfín de aplicaciones existe un sinfín de tornillos y tipos de tornillos de lo
más diverso. Zwick ofrece soluciones mediante muchas sujeciones diferentes y
también con soluciones individuales.
Ensayo de cizallamiento
Aparte de cargas uniaxiales de
tracción, los elementos de sujeción se encuentran sometidos en la práctica a
cargas de cizallamiento que pueden causar una rápida rotura de la unión.
Por ello hay que realizar ensayos de
cizallamiento en piezas unidas o probetas.
Tomemos por ejemplo las uniones
remachadas, en cuyo caso especial la inducción precisa de la carga es de suma
importancia, para que la carga por cizallamiento no sea influenciada por otras
fuerzas colaterales que influyan negativamente sobre los resultados del ensayo.
Zwick especifica con sus clientes la
aplicación concreta para la fijación adecuada de la probeta o del componente e
incluso la fabrica individualmente. Estos dispositivos de ensayo pueden ser
simples o muy complejos, pero siempre cumplen con su objetivo.
Ensayo de fatiga en tornillos
Generalmente, los elementos de unión,
además de estar sometidos a cargas estáticas, a menudo también se someten a
cargas cíclicas. A este grupo de cargas también pertenecen las vibraciones. La
forma más rápida y eficaz de realizar ensayos de fatiga en tornillos es con un
pulsador de alta frecuencia. Con él se pueden aplicar cargas cíclicas con una
c
arga superior de hasta 1000 kN en un rango de frecuencias de hasta aprox. 300
Hz en sujeciones adaptadas especialmente a tornillos u otros elementos de
unión. Gracias al accionamiento magnético que impulsa el sistema y la probeta
por resonancia de forma controlada, este ensayo se realiza con un gasto mínimo
de energía siendo por ello muy económico.
COLUMNAS,
UNIONES Y ESFUERZOS
5.1 Columnas con cargas concéntricas
COLUMNAS
Es un elemento axial sometido a
compresión, lo bastante delgado respecto su longitud, para que abajo la acción
de una carga gradualmente creciente se rompa por flexión lateral o pandeo ante
una carga mucho menos que la necesaria para romperlo por aplastamiento. Las
columnas suelen dividirse en dos grupos: “Largas e Intermedias”. A veces, los
elementos cortos a compresión se consideran como un tercer grupo de columnas.
Las diferencias entre los tres grupos vienen determinadas por su
comportamiento. Las columnas largas re rompen por pandeo o flexión lateral; las
intermedias, por combinación de esfuerzas, aplastamiento y pandeo, y los postes
cortos, por aplastamiento.
CARGAS CONCENTRICAS
Si la excentricidad es pequeña u el
elemento es corto, la flexión lateral es despreciables, y el esfuerzo de
flexión es insignificante comparando con el esfuerzo de compresión directo. Sin
embargo, en un elemento largo, que es mucho mas flexible ya que las flexiones
son proporcionales al cubo de la longitud, con u valor relativamente pequeño de
la carga P puede producirse un esfuerzo de flexión grande, acompañando de un
esfuerzo directo e compresión despreciable. Así en las dos situaciones extremas
una columna corta soporta fundamentalmente el esfuerzo directo de compresión y
una columna larga esta sometida principalmente al esfuerzo de flexión. Cuando
aumenta la longitud de una columna correlativamente las del esfuerzo de
flexión. Por desgracia, en la zona intermedia no es posible determinar
exactamente la forma en que varían estos dos tipos de esfuerzos o la proporción
con la que cada una contribuye al esfuerzo total. Es esta indeterminación la
que da ligar a la gran variedad de formulas para las columnas intermedias.
5.2 Columnas con cargas excéntricas
Cargas excéntricas Las cargas
excéntricas pueden resultar por una carga aplicada fuera del centro de la
zapata o de una carga concéntrica más un momento flexor. Para determinar la
presión debajo de una zapata el momento puede ser removido desplazando la carga
vertical a una locación ficticia con una excentricidad e=m\carga vertical. En
el análisis de cargas excéntricas de zapatas dos diferentes problemas son
confrontados uno.
1.para el propósito de diseño estructural,
la presión contra el fondo de la zapata, comúnmente llamada presión de
contacto, se asume que tiene una distribución plana. Cuando la carga es
aplicada dentro del diamante del área de la zapata, la siguiente formula es
comúnmente aplicada
q= presión sobre el punto de contacto
Q= carga vertical
A=área de la zapata
X y Y= coordenadas del punto en donde
la presión de contacto es calculada
Mx ,My=la carga Q multiplicada por la
excentricidad a los ejes X yY respectivamente
IxIy= momento de inercia del área de
la zapata con respecto a los ejes X y Y respectivamente
La ecuación (6-9) es valida cuando
una de las condiciones siguiente existe a la Zapata es simétrica conrespecto a
los ejes X y Y
La zapata es simétrica con respecto
al eje X y ey =0
La zapata es simétrica con respecto
al ejeYy ex=0
Para zapatas rectangulares la
ecuación (6-9) puede ser escrita de una manera simple
Cuando ex, ey o eb, el exceden un
cierto límite las ecuaciones anteriores dan un valor negativo para q lo que
indica tención entre el suelo y el fondo de la zapata significa que esta carga
q negativa no puede existir por que el suelo no admite esfuerzos a tensión
(unless he footing is weighted down by surchargeloads, the soil cannot be
relied upon for bonding to the footing) la fórmula de flexión anteriores son
aplicables solamente cuando la carga es aplicada dentro del área limitada que
como se sabe es el diamante mostrado en la figura (6-14ª). El procedimiento
para determinar la presión del suelo cuando la carga es aplicada fuera del
diamante es simple en principio, pero laboriosa casos para zapatas
rectangulares y circulares han sido resueltos o trabajados y los diamantes son
mostrados con las áreas.
5.3 RESISTENCIA DE JUNTAS MULTIPLES
La resistencia a cortante en las
juntas secas es una parte importante del diseño de estructuras de dovelas
postensadas. Sin embargo, la formulación de las distintas normativas no se
ajusta al comportamiento de las juntas con llaves múltiples. En este trabajo se
analiza el comportamiento en fractura de las juntas secas con llaves bajo
solicitaciones de cortante, centrándose en la influencia del número de llaves
en la resistencia de la junta y la tensión tangencial media. Para ello, se
modeliza en elementos finitos cuatro tipos de junta, de una a siete llaves. Los
resultados muestran que la tensión tangencial media transferida por la junta
disminuye al aumentar el número de llaves, siendo este efecto menor conforme
aumenta la tensión de compresión actuante en la junta. En este trabajo se
presenta una fórmula de ajuste de los resultados numéricos obtenidos incluyendo
un factor que considera la dependencia del número de llaves.
Sin embargo, la diversa formulación
existente para el cálculo de la resistencia a cortante de las juntas secas con
llaves de las distintas normativas y autores presenta valores muy dispares.
Esto ha dado lugar a estudios experimentales realizados por distintos autores
para analizar el comportamiento de las juntas con llaves (2-6), así como a
diversos modelos numéricos (6-11). La configuración tanto de los ensayos como
de los modelos numéricos recogidos en la bibliografía es muy diferente. Este
hecho dificulta la comparación entre los resultados disponibles, siendo
necesario un estudio pormenorizado para cada caso concreto.
5.4 Clasificación de los materiales
aporte y características
Se entiende como material de
aportación, todo aquel material que se utiliza para la realización de un cordón
de soldadura de buena calidad y donde distinguimos, por un lado, el núcleo del
electrodo y el revestimiento, y, por otro lado, la varilla de aporte y los
fundentes, estos los usaremos en función del tipo de soldadura que vayamos a
realizar.
Algunos de los primeros experimentos
incluyeron envolver el electrodo desnudo con telas de asbesto y algodón
empapadas con silicato de sodio. De estos primeros experimentos surgieron los
electrodos actuales constan de un núcleo de alambre metálico al cual se ha
agregado un recubrimiento de productos químicos seleccionados cuidadosamente.
Clasificación en función del material
del núcleo o el alma
Es lo primero que tenemos que
tener claro a la hora de la elección del electrodo, el tipo de material que
vamos a soldar, para así elegir el electrodo adecuado. Si fuésemos a soldar
aluminio, hay electrodos con el núcleo de aluminio, para fundición tenemos el
monel entre otros, bronce, etc. Las características de cada electrodo vienen
bien especificadas en la caja y son diferentes según el fabricante.
Clasificación en función del
rendimiento
El rendimiento de un electrodo es la
cantidad de material aportada por un electrodo en un cordón de soldadura, donde
interviene, por un lado, el alma o núcleo del electrodo y, por otro lado, los
minerales y materiales que aporta el revestimiento, del que este, está
compuesto. Por lo que podemos decir, que el rendimiento gravimétrico de un
electrodo es la relación existente entre el peso del material que se ha depositado
sobre el metal base y el peso del núcleo del electrodo (sin recubrimiento).
Rendimiento gravimétrico = Peso
material fundido depositado / Peso alma sin punta
5.5 Resistencia de juntas con carga
excéntrica
Cuando la carga sobre una junta
soldada se aplica excéntricamente, el efecto del par o momento debe tomarse en
cuenta, así como la carga directa. El estado de esfuerzo en tal junta es
complicado y es necesario hacer hipótesis simplificadoras.
Cuando una junta consta de varios
cordones de soldadura, es costumbre suponer que el esfuerzo por momento en
cualquier punto es proporcional a la distancia desde el centro de gravedad del
grupo de soldaduras. Suponga que el cordón de soldadura mostrado en la
pertenece a un grupo que forma una junta con el centro de gravedad de todas las
áreas de soldaduras en O. El esfuerzo t por momento actúa perpendicularmente al
radio r sobre el elemento dA de la soldadura. El momento externo o par T es
igual al momento del esfuerzo t integrada sobre todas las soldaduras del punto
La razón Tlr es constante ya que se
supone que el esfuerzo varía directamente con r. La integral en la ecuación (3)
ha sido reemplazada por J, o momento polar de inercia respecto a O para el
grupo de soldaduras. Para obtener el esfuerzo de torsión máximo, debe usarse el
valor de r al punto más alejado del centro de gravedad O. El esfuerzo por carga
directa debe sumarse vectorialmente al esfuerzo por momento para obtener el
esfuerzo resultante. Para cargas estáticas, es práctica usual suponer que el esfuerzo
directo en una
soldadura está uniformemente
distribuido a través de su área.
BIBLIOHGRAFIAS












